Recently, Chinese scientists published a report entitled "[three-body problem - from Newton to supercomputer plus machine learning] on New Astronomy (96: 101850, 2022)( https://sjliao.sjtu.edu.cn/Liao-article/journal/2022/2.pdf ) ”Based on machine learning and a highly accurate numerical algorithm (CNS), a roadmap for solving the famous "three body problem" periodic orbit is proposed** The first author of this article is liaoshijun from shanghaijiaotonguniversity, the second author is lixiaoming from Jinan University, and the third author is Yang Yu, a doctoral student from shanghaijiaotonguniversity.
How do three planets of any mass move under the action of gravity? Newton put forward the famous "three body problem" in 1687, which has been widely concerned by the international academic community for more than 300 years, and has become one of the most famous scientific problems in history. According to the topological classification of periodic orbits of three body problems proposed by Montgomery, from 1687 to 1993, only three families of periodic orbits of three body problems have been found, namely: (1) Euler Lagrange family (exact solution, Euler 1740, Lagrange 1772), (2) BBH family (numerical solution, brocke 1975, brocke and Boggs 1975, hadjidemetriou 1975, H é non 1976) (3) figure-8 family (numerical solution, Moore 1993). Why is the periodic orbit of the three body problem so difficult to find? In 1890 Poincare found that the trajectory of the three body system generally does not have the first kind of integral (that is, the analytical solution generally does not exist), and is very sensitive to the initial conditions: any small disturbance will be exponentially amplified, resulting in the rapid separation of its trajectory and the true solution. The sensitivity of this trajectory to small disturbances was rediscovered by Lorenz in 1963 and the famous "Butterfly Effect" was proposed. The discovery of this characteristic marks the birth of "chaotic dynamics", which, together with quantum mechanics and relativity, is considered to be one of the three greatest physical theories in the 20th century. It is precisely because of the chaotic nature of the three body problem that it is difficult to obtain the accurate orbit of the three body system in a long time domain even using the traditional numerical methods. This explains why only three families of periodic orbits of the three body problem have been found more than 300 years after Newton proposed the three body problem in 1687.
As we all know, there are errors in any numerical calculation. Lorenz found in 1989 that due to the "Butterfly Effect", small numerical errors, as a small artificial disturbance, will also lead to the rapid deviation of the numerical solution (trajectory) of the chaotic system. In particular, Lorenz found that if the chaotic dynamic system is solved by double precision numerical method, the trajectory of the chaotic system will not converge no matter how short the time step is. This can well explain why, when the computer performance reached 10billion orders per second in 2013, only 11 families of new periodic orbits of the three body problem were found.
In 2009, liaoshijun of shanghaijiaotonguniversity proposed a strategy to numerically solve the convergence trajectory of chaotic dynamic systems, namely clean numerical simulation (CNS). CNS not only reduces the truncation error of numerical simulation, but also uses multiple precision data instead of double precision to reduce the whole numerical error to an arbitrary small, so that the convergent numerical solution of chaotic system can be obtained in a sufficiently long time domain. Therefore, CNS theoretically paves the way for accurately obtaining the periodic orbits of the three body problem. In 2017, liaoshijun's team successfully obtained 695 family periodic orbits (Science China – physics, mechanics & astronomy, 2017) for three body problems with equal mass and zero angular momentum by combining CNS with search method and Newton Raphson iteration method, including Š Uvakov and dmitra š inovi ć In 2013, 11 families of periodic orbits (all with periods less than 100) and 466 families of periodic orbits with periods greater than 100 were found, which has never been reported. In 2018, liaoshijun's team cooperated with jingyipeng, an academician of the school of physics and astronomy of Shanghai Jiao Tong University, to further successfully obtain 1349 new periodic solutions of two three body systems with equal mass and zero angular momentum by using CNS, search method and Newton Raphson iteration method (Publications of the Asian Society of Japan, 2018). In 2021, liaoshijun and lixiaoming cooperated with each other to combine CNS with the comsolution method and Newton Raphson iteration method to successfully obtain 135445 periodic solutions of the three body system with any unequal mass from a known periodic orbit of the three body problem with the same mass (Science China – physics, mechanics & astronomy, 2021), The number of periodic orbits of three body problems is increased by several orders of magnitude, which proves the effectiveness of CNS in solving periodic orbits of three body problems (especially long periodic orbits). It is worth noting that, unlike the hierarchical structure of the sun earth moon, these 135445 periodic orbits are non hierarchical, and many of them are stable. Their mass range is similar to that of the first planet outside the solar system (with hierarchical structure) discovered by Michel mayor and Didier Queloz, winners of the Nobel Prize in physics in 2019, Therefore, it is very likely that it does exist in the universe and may be observed by astronomers.
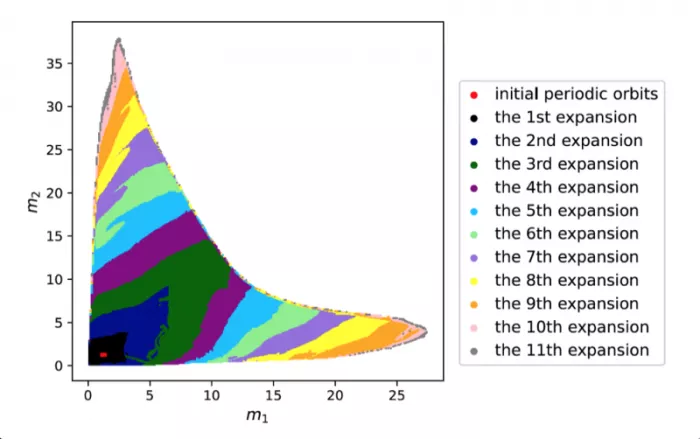
Figure 1: using machine learning to find periodic orbits of different star masses of the same family of three body systems. The red area in the lower left corner is a few known periodic orbits obtained by traditional methods. The same color represents the largest region of periodic orbit that can be found by machine learning for the same extrapolation. M1 and M2 are the masses of two planets (M3 = 1)
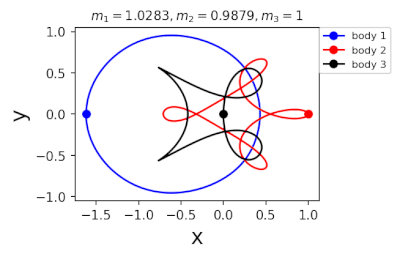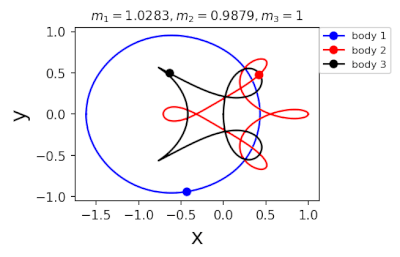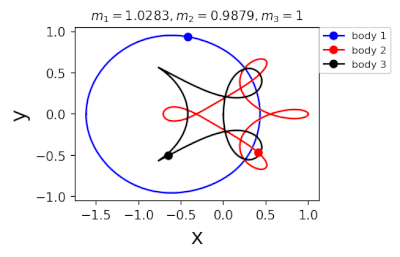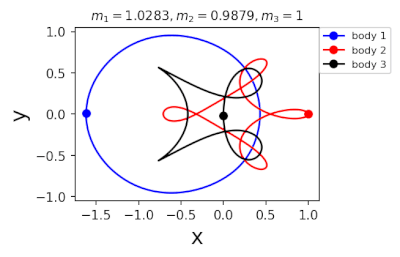
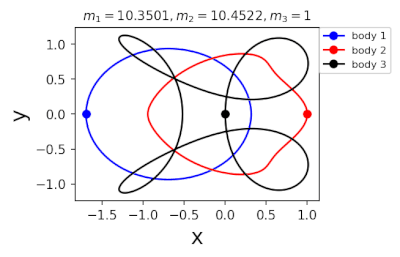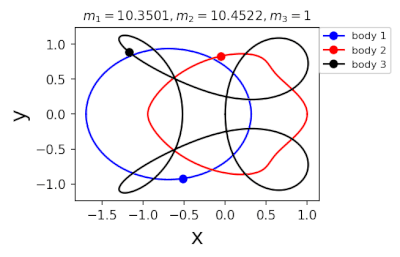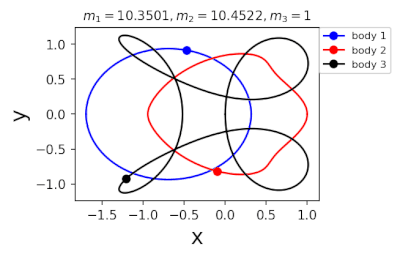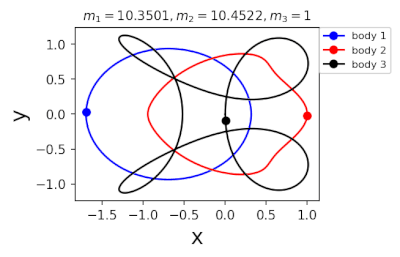
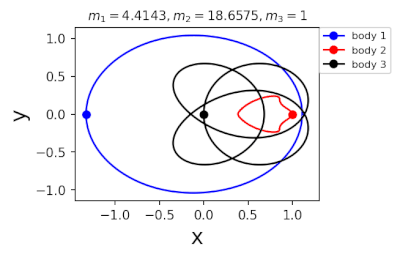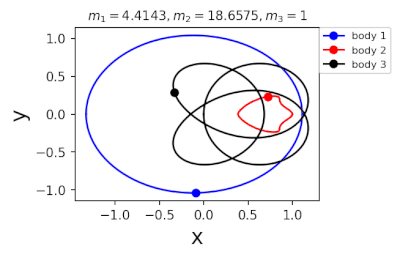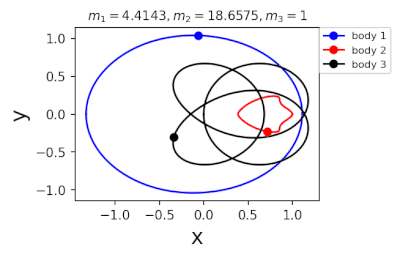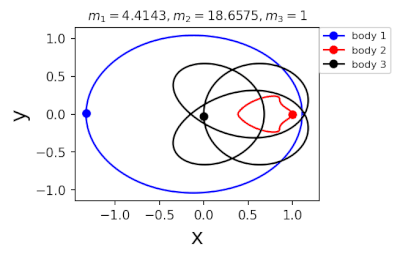
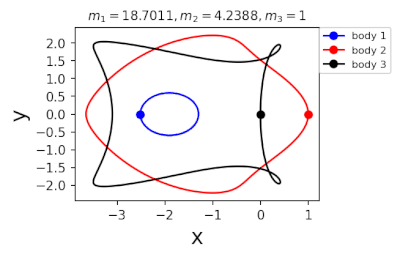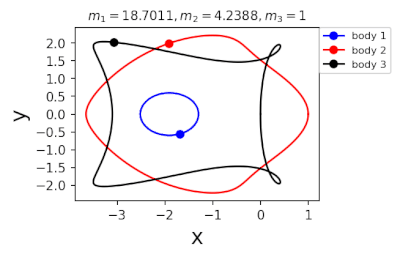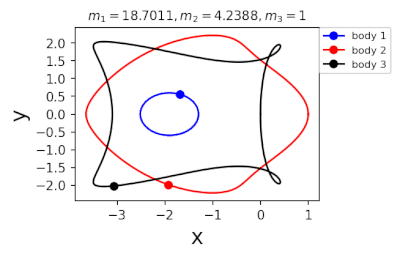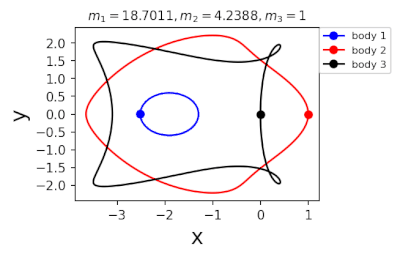
In 2022, in order to further greatly improve the calculation efficiency, liaoshijun, lixiaoming and Yang Yu combined CNS with machine learning and Newton Raphson iteration, using the initial conditions of a few periodic orbits obtained by the above traditional methods as the preliminary training set, and using machine learning to give the estimated values of the initial conditions of the periodic orbits of the three body problem when the satellite mass is extrapolated, and then using CNS to obtain the star motion convergence trajectories with high accuracy, Newton Raphson is used to modify the initial conditions and find the exact periodic orbit iteratively; All new periodic orbits obtained by each extrapolation are used to form a larger training set to continuously increase the extrapolation range of the planet's mass. At the same time, the prediction accuracy of the machine learning model for the initial value of periodic orbits is continuously improved until all periodic orbits of different masses of the three body problem of this family are found, as shown in Figure 1. Finally, the machine learning model trained with all the periodic orbits thus obtained can accurately predict the initial conditions, period and stability of the periodic orbits for a three body problem with any mass (in the region where the periodic orbits exist), as shown in Figure 2. The strategy based on CNS and machine learning improves the computational efficiency by several orders of magnitude, and puts forward a new road map for efficiently obtaining the periodic orbit of the three body problem. The paper was published in the International Astronomical Journal New Astronomy in 2022( https://doi.org/10.1016/j.newast.2022.101850 ) , its related machine learning program and periodic orbit can be found in GitHub( https://github.com/sjtu-liao/three-body ) Free download.
It is worth noting that due to the adoption of CNS, the (dimensionless) periodic orbit obtained by liaoshijun's team and its collaborators has reached 60 bit effective accuracy: even if the cosmic diameter (930 light years) is taken as the characteristic length, the accuracy of its initial position has reached the order of 1.0e-41 meters, which is far less than the Planck length (1.62e-35 meters), which is the minimum length with physical significance. Therefore, from a physical point of view, further improving the accuracy of the calculation results has no physical significance, although it is easy to do so with CNS. Therefore, the accuracy of the periodic orbit of the three body problem obtained by using CNS is so high that it is an accurate orbit in the physical sense. In other words, physically speaking, the exact solution of the periodic orbit of the three body problem can be obtained by using CNS!
Liaoshijun, lixiaoming and Yang Yu proposed a roadmap for solving periodic orbits of three body problems based on CNS and machine learning, which improved the computational efficiency by several orders of magnitude and paved the way for obtaining massive and (physically) accurate periodic orbits of three body problems. Today, with high-performance computers, there are no obstacles that can prevent humans from obtaining massive (physical sense) accurate periodic orbits of the three body problem. The solution of the three body problem essentially depends on high-performance computers and mathematical methods. Reviewing the history of solving the famous three body problem for more than 300 years, people can not help but thank those great mathematicians, physicists and engineering technicians, especially Poincare, who created "chaotic dynamics", Turing, the father of computer and artificial intelligence, von Neumann, who proposed the modern computer architecture, and Jack s. Kilby, who participated in the invention of integrated circuits and won the Nobel Prize in physics in 2000. The solution of the classical problem of periodic orbit of the three body problem is a model of the integration of theory and technology.
The solution of periodic orbit of three body problem proves the effectiveness and potential of CNS in solving complex chaotic problems. Theoretically, CNS can be applied to the solution of periodic orbits of N-body problem (n > 3), the accurate numerical simulation of galaxy evolution, the accurate numerical simulation of turbulence, and so on.
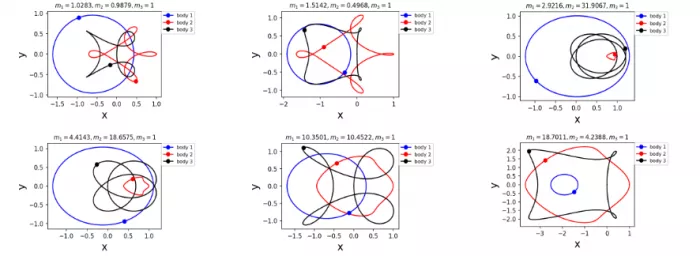
Figure 2: periodic orbits simulated by periodic solutions of three body problems with different mass predicted by machine learning. Blue line: the first planet; Red line: the second planet; Black line: the third planet.


[about the author]

Dr. liaoshijun, Chair Professor, School of marine and architectural engineering, Shanghai Jiaotong University
Adjunct professor, School of physics and astronomy, Shanghai Jiaotong University

Dr. lixiaoming, associate professor, School of mechanics and architectural engineering, Jinan University

Yang Yu, doctoral candidate, School of marine and architectural engineering, Shanghai Jiaotong University